1. BCD
Código BCD (Binary-Coded Decimal (BCD) o Decimal codificado). Binario es un estándar para representar números decimales en el sistema binario, en donde cada dígito decimal es codificado con una secuencia de 4 bits.
Con esta codificación especial de los dígitos decimales en el sistema binario, se pueden realizar operaciones aritméticas como suma, resta, multiplicación y división de números en representación decimal, sin perder en los cálculos la precisión ni tener las inexactitudes en que normalmente se incurren con las conversiones de decimal a binario puro y de binario puro a decimal.
La conversión de los números decimales a BCD y viceversa es muy sencilla, pero los cálculos en BCD se llevan más tiempo y son algo más complicados que con números binarios puros.
-Ejemplo:
La codificación en BCD del
número decimal 59237 es:
Decimal:
5 9
2 3
7
BCD:
0101 1001 0010
0011 0111
La representación anterior
(en BCD) es diferente de la representación del mismo número decimal en binario
puro:
11100111 01100101
2. ASCII
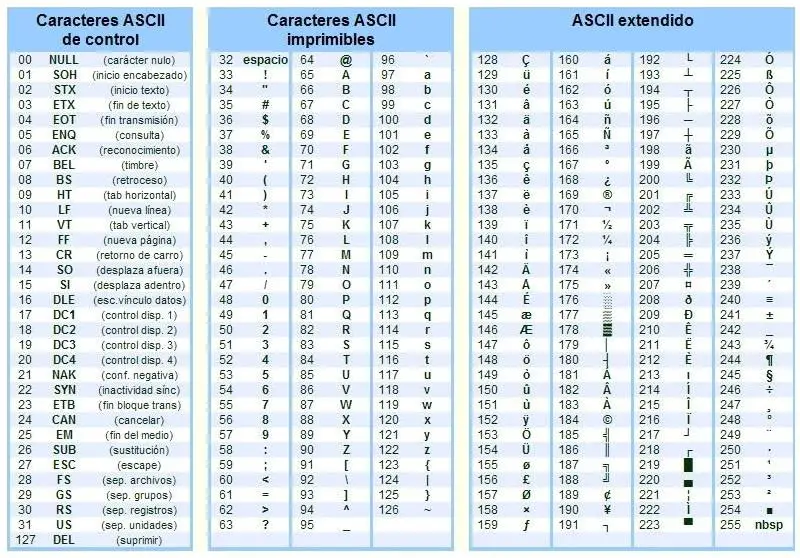
El ASCII en informática se conoce
como código fuente al texto desarrollado
en un lenguaje de programación que debe ser compilado o desarrollado para poder
ejecutar en un ordenador, que es una presentación de los caracteres
alfanuméricos que es cuando está formado por letras y números y se hace fácil
para la comunicación entre los diferentes dispositivos digitales.
El código ASCII representa un conjunto de
números desde el 0 al 127, en escala decimal, para el procesador que se
trata de una cadena binaria que está compuesto por dos elementos o unidades de
7 dígitos, donde 127 se expresa como 1111111 y resulta especialmente útil para
la realización de los sitios web.
También
existen muchos formularios que pueden llenar los usuarios y sobre todo si la
página tiene diferentes versiones en varios idiomas que son importantes y puede
ser muy meticuloso en el procesamiento del texto ingresado para asegurar que se
almacene en la base de datos y de esa forma pueda revisar la información y no
existan errores a la hora de imprimir los caracteres especiales, porque la
combinación de caracteres se emplea para crear y entender mensajes secretos.
3. CÓDIGO GRAY
Consiste en una ordenación de <math>2^n</math> números binarios de tal forma que cada número sólo tenga un dígito binario distinto a su predecesor. Esta técnica de codificación se originó cuando los circuitos lógicos digitales se realizaban con válvulas de vacío y dispositivos electromecánicos. Los contadores necesitaban potencias muy elevadas a la entrada y generaban picos de ruido cuando varios bits cambiaban simultáneamente.
El uso de código Gray garantizó que en cualquier transición variaría tan sólo un bit. En la actualidad, el código Gray se sigue empleando para el diseño de cualquier circuito electrónico combinacional mediante el uso de un Mapa de Karnaugh, ya que el principio de diseño de buscar transiciones más simples y rápidas entre estados sigue vigente, a pesar de que los problemas de ruido y potencia se hayan reducido.
Hay varios algoritmos para generar una secuencia de código Gray (y varios códigos posibles resultantes, en función del orden que se desee seguir), pero el más usado consiste en cambiar el bit menos significativo que genera un nuevo código. Este es un código gray de cuatro bits generado con dicho algoritmo:


Para convertir un número binario (en Base 2) a código Gray, simplemente se le aplica una operación XOR con el mismo número desplazado un bit a la derecha, sin tener en cuenta el acarreo.
Ejemplo:
1010 (Base 2) a
gray
1010
101
----
1111
|
4. Código FIELDATA
Es el juego de caracteres original utilizado internamente en UNIVAC ordenadores de la serie 1100 , que representa la sexta parte de la palabra de 36 bits de ese equipo. El sucesor directo del UNIVAC 1100 es las Unisys serie 2.200 computadoras, que utilizan Fieldata hasta nuestros días (aunque ASCII ahora también es común con cada carácter codificado en 1/4 de una palabra, o 9 bits). Debido a que algunos de los personajes Fieldata no están representados en ASCII, el Unisys 2200 utiliza "^" '"' y los caracteres '_' para los códigos 04, 076 y 077 (octal), respectivamente.
El proyecto Fieldata corrió desde 1956 hasta que fue detenido durante una reorganización en 1962.
Caracteres Fieldata:
| Bit (1) | Indicator Bits (2) | Detail Bits (4) | Binary Bits (7) | Decimal | Octal | Glyph | Name |
| 0 | 00 | 0000 | 0000000 | 0 | 0 | @ | MasterSpace |
| 0 | 00 | 0001 | 0000001 | 1 | 1 | [ | |
| 0 | 00 | 0010 | 0000010 | 2 | 2 | ] | |
| 0 | 00 | 0011 | 0000011 | 3 | 3 | # | |
| 0 | 00 | 0100 | 0000100 | 4 | 4 | Δ | Delta |
| 0 | 00 | 0101 | 0000101 | 5 | 5 | Blank | |
| 0 | 00 | 0110 | 0000110 | 6 | 6 | A | |
| 0 | 00 | 0111 | 0000111 | 7 | 7 | B | |
| 0 | 00 | 1000 | 0001000 | 8 | 10 | C | |
| 0 | 00 | 1001 | 0001001 | 9 | 11 | D | |
| 0 | 00 | 1010 | 0001010 | 10 | 12 | E | |
| 0 | 00 | 1011 | 0001011 | 11 | 13 | F | |
| 0 | 00 | 1100 | 0001100 | 12 | 14 | G | |
| 0 | 00 | 1101 | 0001101 | 13 | 15 | H | |
| 0 | 00 | 1110 | 0001110 | 14 | 16 | I | |
| 0 | 00 | 1111 | 0001111 | 15 | 17 | J | |
| 0 | 01 | 0000 | 0010000 | 16 | 20 | K | |
| 0 | 01 | 0001 | 0010001 | 17 | 21 | L | |
| 0 | 01 | 0010 | 0010010 | 18 | 22 | M | |
| 0 | 01 | 0011 | 0010011 | 19 | 23 | N | |
| 0 | 01 | 0100 | 0010100 | 20 | 24 | O | |
| 0 | 01 | 0101 | 0010101 | 21 | 25 | P | |
| 0 | 01 | 0110 | 0010110 | 22 | 26 | Q | |
| 0 | 01 | 0111 | 0010111 | 23 | 27 | R | |
| 0 | 01 | 1000 | 0011000 | 24 | 30 | S | |
| 0 | 01 | 1001 | 0011001 | 25 | 31 | T | |
| 0 | 01 | 1010 | 0011010 | 26 | 32 | U | |
| 0 | 01 | 1011 | 0011011 | 27 | 33 | V | |
| 0 | 01 | 1100 | 0011100 | 28 | 34 | W | |
| 0 | 01 | 1101 | 0011101 | 29 | 35 | X | |
| 0 | 01 | 1110 | 0011110 | 30 | 36 | Y | |
| 0 | 01 | 1111 | 0011111 | 31 | 37 | Z | |
| 0 | 10 | 0000 | 0100000 | 32 | 40 | ) | |
| 0 | 10 | 0001 | 0100001 | 33 | 41 | - | |
| 0 | 10 | 0010 | 0100010 | 34 | 42 | + | |
| 0 | 10 | 0011 | 0100011 | 35 | 43 | < | |
| 0 | 10 | 0100 | 0100100 | 36 | 44 | = | |
| 0 | 10 | 0101 | 0100101 | 37 | 45 | > | |
| 0 | 10 | 0110 | 0100110 | 38 | 46 | & | |
| 0 | 10 | 0111 | 0100111 | 39 | 47 | $ | |
| 0 | 10 | 1000 | 0101000 | 40 | 50 | * | |
| 0 | 10 | 1001 | 0101001 | 41 | 51 | ( | |
| 0 | 10 | 1010 | 0101010 | 42 | 52 | % | |
| 0 | 10 | 1011 | 0101011 | 43 | 53 | : | |
| 0 | 10 | 1100 | 0101100 | 44 | 54 | ? | |
| 0 | 10 | 1101 | 0101101 | 45 | 55 | ! | |
| 0 | 10 | 1110 | 0101110 | 46 | 56 | , | |
| 0 | 10 | 1111 | 0101111 | 47 | 57 | \ | |
| 0 | 11 | 0000 | 0110000 | 48 | 60 | 0 | |
| 0 | 11 | 0001 | 0110001 | 49 | 61 | 1 | |
| 0 | 11 | 0010 | 0110010 | 50 | 62 | 2 | |
| 0 | 11 | 0011 | 0110011 | 51 | 63 | 3 | |
| 0 | 11 | 0100 | 0110100 | 52 | 64 | 4 | |
| 0 | 11 | 0101 | 0110101 | 53 | 65 | 5 | |
| 0 | 11 | 0110 | 0110110 | 54 | 66 | 6 | |
| 0 | 11 | 0111 | 0110111 | 55 | 67 | 7 | |
| 0 | 11 | 1000 | 0111000 | 56 | 70 | 8 | |
| 0 | 11 | 1001 | 0111001 | 57 | 71 | 9 | |
| 0 | 11 | 1010 | 0111010 | 58 | 72 | ' | |
| 0 | 11 | 1011 | 0111011 | 59 | 73 | ; | |
| 0 | 11 | 1100 | 0111100 | 60 | 74 | / | |
| 0 | 11 | 1101 | 0111101 | 61 | 75 | . | |
| 0 | 11 | 1110 | 0111110 | 62 | 76 | ¤ | Lozenge |
| 0 | 11 | 1111 | 0111111 | 63 | 77 | ≠ | Not Equal |
| 1 | 00 | 0000 | 1000000 | 64 | 100 | Blank/Idle | |
| 1 | 00 | 0001 | 1000001 | 65 | 101 | Control Upper Case | |
| 1 | 00 | 0010 | 1000010 | 66 | 102 | Control Lower Case | |
| 1 | 00 | 0011 | 1000011 | 67 | 103 | Control Tab | |
| 1 | 00 | 0100 | 1000100 | 68 | 104 | Control Carriage Return | |
| 1 | 00 | 0101 | 1000101 | 69 | 105 | Control Space | |
| 1 | 00 | 0110 | 1000110 | 70 | 106 | a | |
| 1 | 00 | 0111 | 1000111 | 71 | 107 | b | |
| 1 | 00 | 1000 | 1001000 | 72 | 110 | c | |
| 1 | 00 | 1001 | 1001001 | 73 | 111 | d | |
| 1 | 00 | 1010 | 1001010 | 74 | 112 | e | |
| 1 | 00 | 1011 | 1001011 | 75 | 113 | f | |
| 1 | 00 | 1100 | 1001100 | 76 | 114 | g | |
| 1 | 00 | 1101 | 1001101 | 77 | 115 | h | |
| 1 | 00 | 1110 | 1001110 | 78 | 116 | i | |
| 1 | 00 | 1111 | 1001111 | 79 | 117 | j | |
| 1 | 01 | 0000 | 1010000 | 80 | 120 | k | |
| 1 | 01 | 0001 | 1010001 | 81 | 121 | l | |
| 1 | 01 | 0010 | 1010010 | 82 | 122 | m | |
| 1 | 01 | 0011 | 1010011 | 83 | 123 | n | |
| 1 | 01 | 0100 | 1010100 | 84 | 124 | o | |
| 1 | 01 | 0101 | 1010101 | 85 | 125 | p | |
| 1 | 01 | 0110 | 1010110 | 86 | 126 | q | |
| 1 | 01 | 0111 | 1010111 | 87 | 127 | r | |
| 1 | 01 | 1000 | 1011000 | 88 | 130 | s | |
| 1 | 01 | 1001 | 1011001 | 89 | 131 | t | |
| 1 | 01 | 1010 | 1011010 | 90 | 132 | u | |
| 1 | 01 | 1011 | 1011011 | 91 | 133 | v | |
| 1 | 01 | 1100 | 1011100 | 92 | 134 | w | |
| 1 | 01 | 1101 | 1011101 | 93 | 135 | x | |
| 1 | 01 | 1110 | 1011110 | 94 | 136 | y | |
| 1 | 01 | 1111 | 1011111 | 95 | 137 | z | |
| 1 | 10 | 0000 | 1100000 | 96 | 140 | Dial 0 | |
| 1 | 10 | 0001 | 1100001 | 97 | 141 | Dial 1 | |
| 1 | 10 | 0010 | 1100010 | 98 | 142 | Dial 2 | |
| 1 | 10 | 0011 | 1100011 | 99 | 143 | Dial 3 | |
| 1 | 10 | 0100 | 1100100 | 100 | 144 | Dial 4 | |
| 1 | 10 | 0101 | 1100101 | 101 | 145 | Dial 5 | |
| 1 | 10 | 0110 | 1100110 | 102 | 146 | Dial 6 | |
| 1 | 10 | 0111 | 1100111 | 103 | 147 | Dial 7 | |
| 1 | 10 | 1000 | 1101000 | 104 | 150 | Dial 8 | |
| 1 | 10 | 1001 | 1101001 | 105 | 151 | Dial 9 | |
| 1 | 10 | 1010 | 1101010 | 106 | 152 | Start of Control Block | |
| 1 | 10 | 1011 | 1101011 | 107 | 153 | Start of Block | |
| 1 | 10 | 1100 | 1101100 | 108 | 154 | Spare | |
| 1 | 10 | 1101 | 1101101 | 109 | 155 | Spare | |
| 1 | 10 | 1110 | 1101110 | 110 | 156 | Spare | |
| 1 | 10 | 1111 | 1101111 | 111 | 157 | Spare | |
| 1 | 11 | 0000 | 1110000 | 112 | 160 | Ready to Transmit | |
| 1 | 11 | 0001 | 1110001 | 113 | 161 | Ready to Receive | |
| 1 | 11 | 0010 | 1110010 | 114 | 162 | Not Ready to Receive | |
| 1 | 11 | 0011 | 1110011 | 115 | 163 | End of Blockette | |
| 1 | 11 | 0100 | 1110100 | 116 | 164 | End of Block | |
| 1 | 11 | 0101 | 1110101 | 117 | 165 | End of File | |
| 1 | 11 | 0110 | 1110110 | 118 | 166 | End of Control Block | |
| 1 | 11 | 0111 | 1110111 | 119 | 167 | Acknowledge Receipt | |
| 1 | 11 | 1000 | 1111000 | 120 | 170 | Repeat Block | |
| 1 | 11 | 1001 | 1111001 | 121 | 171 | Spare | |
| 1 | 11 | 1010 | 1111010 | 122 | 172 | Interpret Sign | |
| 1 | 11 | 1011 | 1111011 | 123 | 173 | Non-Interpret Sign | |
| 1 | 11 | 1100 | 1111100 | 124 | 174 | Control Word Follows | |
| 1 | 11 | 1101 | 1111101 | 125 | 175 | S.A.C. | |
| 1 | 11 | 1110 | 1111110 | 126 | 176 | Special Character | |
| 1 | 11 | 1111 | 1111111 | 127 | 177 | Delete |
5. CÓDIGO BINARIO
El código binario es el sistema de representación de textos, o procesadores de instrucciones de ordenador utilizando el sistema binario (sistema numérico de dos dígitos, o bit: el "0" y el "1"). En informática y telecomunicaciones, el código binario se utiliza con variados métodos de codificación de datos, tales como cadenas de caracteres, o cadenas de bits. Estos métodos pueden ser de ancho fijo o ancho variable.
En un código binario de ancho fijo, cada letra, dígito, u otros símbolos, están representados por una cadena de bits de la misma longitud, como un número binario que, por lo general, aparece en las tablas en notación octal, decimal o hexadecimal.


