Método de Quine-McCluskey

Desarrollado por Willard Van Orman Quine y Edward J. McCluskeyes, para la simplificación de funciones booleanas respaldado por un procedimiento  algorítmico dando así un resultado mas normalizado y minimizado, es similar al mapa de Karnaugh, pero su forma tabular lo hace más eficiente para su implementación en lenguajes computacionales.

El método de Quine – McCluskey es útil para minimizar expresiones algebraicas que describen circuitos lógicos electrónicos.

La cualidad de este método es que es un método tabular y gráfico, ideal para programarlo y obtener así un algoritmo que permita la obtención de expresiones algebraicas minimizadas del circuito en cuestión. 

Pasos para resolver el método

Sea K un álgebra de Boole y f una función booleana de orden n sobre K. Denotamos por B = {0, 1}. Para obtener una expresión simplificada de f realizamos los siguientes pasos: 

Paso 1 

Para saber si podemos aplicar el método de Quine McCluskey es necesario (lo pondré en negritas y en mayúsculas) TENER LA FUNCIÓN EXPRESADA EN FORMA CANÓNICA, ya sea expresada con una suma de minitérminos o un producto de maxitérminos. En este ejemplo vamos a usar minitérminos.

Paso 2 

Aquí vamos a determinar en una tabla (ya empezamos a hacer tablas) el número de “1” que tiene cada término involucrado en la función.

Paso 3 

Aquí vamos a hacer una tabla más (y las que faltan), en ésta vamos a agregar una columna donde vamos a marcar qué términos se combinan y cuáles no. Los vamos a agrupar por el número de unos que contienen. 

Paso 4 

Con la tabla pasada que creamos, vamos a crear ¡Más tablas! Vamos a formar nuevas tablas combinando lo términos entre grupos de unos. Para que dos términos de puedan combinar, vamos a observar sus combinaciones binarias (los unos y los ceros) y si entre ellas existe SÓLO LA DIFERENCIA DE UN DÍGITO, entonces estos términos se combinan y se marcan con una palomita.

¿Te das cuenta de cómo se hacen las combinaciones? Es muy fácil. Por ejemplo, en la combinación del 1 y 3, si notas en la tabla del paso 3, te darás cuenta que comparten un “1” en el bit D y la diferencia de un dígito de encuentra en el bit C del término 3. Eso mismo vamos a hacer con las demás combinaciones.

Paso 5 

En este paso vamos a etiquetar a los implicantes primos que encontramos en las tablas, o sea, los asteriscos que tienen las tablas. Y después, procederemos a marcar con una palomita, cada uno de los términos que se combinaron en cada implicante primo.

Paso 6 – 

Vamos a hacer un análisis por columna y aquella que sólo tenga una palomita, la vamos a encerrar en un círculo.

Paso 7

Aquí realizaremos un recorrido por cada uno de los renglones donde aparezca al menos una marca y se marcará en el último renglón todas aquellas columnas que tienen marcas

Paso 8 

Si todas las columnas en el último renglón tienen marcas, se llegó al final de la segunda etapa. Amiga, amigo, terminaste de simplificar por el método de Quine McCluskey.

La función reducida estará formada por todos aquellos implicantes primos que al menos una de sus marcas se encuentra encerrada (echa ojo a las tablas del paso 4):

Minimización por el método de QUINE-McCLUSKEY

Se tienen dos formas de desarrollar el método de Quine-McCluskey: con una combinación binaria y una combinación decimal

Combinación Binaria

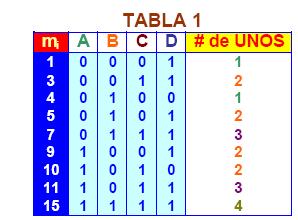
Sea la función: F(A, B, C, D) = Sm (1, 3, 4, 5, 7, 9, 10, 11, 15) La TABLA 1 presenta la lista de los minitérminos, expresados en forma binaria e indica el número de UNOS que estos contienen:

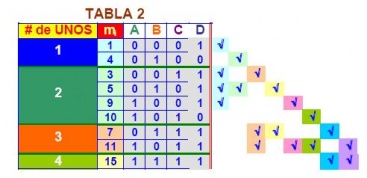
En la TABLA 2, se agrupan los minitérminos con el mismo número de UNOS.

De la TABLA 2, se combinan los términos que tienen un solo UNO con los que tienen dos UNOS, los que tienen dos UNOS con los que tienen tres UNOS y así sucesivamente. Dos términos se podrán combinar siempre y cuando exista un solo cambio entre ellos, es decir, cuando el lugar en que estén colocados los UNOS coincidan. Por ejemplo, los términos 1 y 3 se combinan debido a lo siguiente:

ABCD + ABCD = ABD(C+ C) = ABXD 0001 0011 00X1

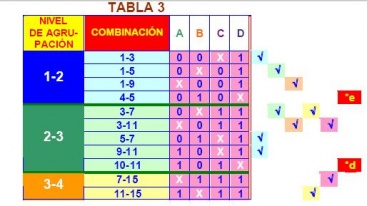
O sea que entre los términos 1 y 3 se eliminó la variable C. Haciendo lo mismo con los demás términos, se obtiene la TABLA 3.

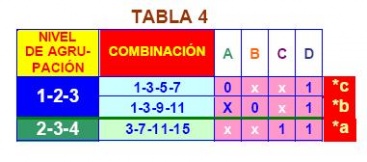
Los términos que en su fila tienen Ö, son los que se combinaron. Los términos con *, son los que no pudieron combinarse, es decir, aquellos que en su fila no tienen Ö. A estos términos se les denomina IMPLICANTES PRIMOS. Para la TABLA 4, se combinan los niveles de agrupación 1-2 con 2-3 y 2-3 con 3-4, tomando en cuenta que coincidan tanto las x como los UNOS.

Como ya se indicó, los implicantes primos son términos que no se combinan con ningún otro, por tanto pueden formar parte de la función reducida. Para determinar cuáles de los implicantes primos forman parte de la función reducida, se hace la siguiente tabla, llamada de implicantes primos.

Este  método lo vamos a dividir en dos etapas:

1. Primera etapa: a través de las tablas de verdad buscaremos aquellos términos que pueden pertenecer a la función simplificada ( tal y como lo hacíamos en los mapas de karnaugh).
2. Segunda etapa: Escoger entre los números o términos a los que den una expresión simplificada o minimizada.

Ventajas del método: 

• Es directo

• Seguro

• Se puede utilizar en muchas variables, no hay limitaciones de números.

• Utiliza álgebra de boole para dar respuesta a la ecuación.

• Es ordenado

• Se reduce la variable automáticamente, sin proceso alguno

Desventajas del método: 

• Es muy largo según las variables ingresadas.

• Requiere mucha paciencia.

• Tiende a haber equivocaciones.

• Es extenso así tenga pocas variables.